What are fractals? Where do we find them? How are they made? Why should we care about them? What are they good for? These are some of the questions we’ll be looking at through this online fractal course.

Fractals are complex patterns that show the same details at different scales. This means you can zoom into a fractal and find the same pattern deeper and deeper.

Although fractals are very complex shapes, they are formed by repeating a simple process over and over. Play with the fractal below by dragging the dots.

We can find fractals all over the natural world, from tiny patterns like seashells up to the giant spirals of the galaxies. Trees, river networks, mountains, coastlines, lightning bolts, blood vessels, flowers, etc are all examples of natural fractals. We can look at a fractal as a picture that tells a story of the natural processes that formed it. One of the great things about fractals is that even if you don’t think you know anything at all about fractals yet, you actually already do, because you’ve grown up in a world full of fractals.

We will also discover fractals made by computer, using simple algebraic equations calculated over and over. These fractals are particularly fun because they go on forever – that is they are infinitely complex. Explore the edge of the Mandelbrot Fractal below by clicking on it.

Both natural and mathematical fractals can be extremely beautiful, and one of the extraordinary things about learning fractals is to discover that science, math and art are intimately related.

Fractals are full of meaning. They are patterns that tell stories. Fractals are the pictures of Chaos Theory, the study of unpredictable, dynamic systems. We will use fractals to learn the fundamental lesson of Chaos Theory, that small changes can lead to big differences

Finally, fractals can be very useful, and we will some examples of fractals in engineering, medicine, electronics, and even in the design of cities.

Studying fractals can lead to a deeper understanding of the patterns of nature and the ways in which a wide range of seemingly different systems are actually interconnected.

Enjoy!

“Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.”

Perhaps the most remarkable thing about the study of fractals is that there are fractal patterns all around us! Even if you don’t think you know anything at all about fractals yet, you actually already do, because you’ve grown up in a world full of fractals. In this first chapter we will first learn about natural Branching fractals, and then about Spiral fractals.

Perhaps the most remarkable thing about the study of fractals is that there are fractal patterns all around us! Even if you don’t think you know anything at all about fractals yet, you actually already do, because you’ve grown up in a world full of fractals. In this first chapter we will first learn about natural Branching fractals, and then about Spiral fractals.

Fractal Trees

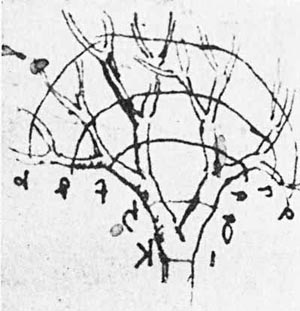
The plant kingdom is full of fractal patterns, and while we have only started calling these patterns ‘fractal’ since the 1970’s, people have been observing these kinds of patterns for much longer. Perhaps the first description of a fractal pattern in nature came from the great artist and scientist Leonardo da Vinci in the 15th century.

Elm trees. Photo courtesy of Jonathan Wolfe.

There are a few things to notice about the fractal structure of a tree. First of all, a tree is approximately self-similar. That is, a small piece of the tree looks somewhat like an entire tree. Secondly, while a tree is a large, complex object, it is formed by repeating a simple process over and over again. This is a basic principle that we will see over and over again in all the various fractals we’ll encounter, whether in nature, on paper, or in a computer.

The essential, basic process by which a tree grows is this:

A sprout comes out of the ground, and then splits into branches. Each of these branches then splits again into new branches, and each of these branches splits again into new branches. At each point in this process, it is as if two new, smaller trees emerge, and the new branches can be thought of as the trunks of the next generation of trees. So a large tree can be seen as a collection of many smaller trees of various sizes. Thus the repetition of branching that forms the tree also generates the tree’s self-similarity. In plant science, the branching points are called ‘nodes’, and the branches themselves ‘internodes’. In general mathematical terms, we refer to the branching points as “bifurcations” and the internodes as… “branches.” We will see many examples of bifurcations in our exploration of fractals.

Note: Natural fractals such as trees and ferns do NOT keep repeating their patterns forever. The mathematical fractals we will encounter in a few weeks, such as the Mandelbrot Set, DO go on forever. At some point, the fractal repetition breaks down in natural patterns, and they cease to be fractals.

We can find fractal patterns over a wide range of scales in nature, and we can see a similar branching pattern in the veins of a tree’s leaves. We will soon see examples of natural fractal patterns that are much larger – and smaller – than these.

Questions:

Refer to Leonardo’s sketch of a tree above. Let’s call the tree trunk the zero order branch. When it splits in two, we’ll call these the first order branching, and there are two of them. When these two branch again, it is called the third order branching, and there are four of these 3rd order branches.

What is the highest order of branching that Leonardo shows in his drawing? [ ]
How many of the highest order branches are there [ ]
If a tree followed this same progression, and had 8 orders of branching, how many 8th order branches would it have? [ ]
If this hypothetical tree had 8 orders of branching, how many branches total would there be (8’th order + 7th order + 6th order, etc)? [ ]

Fractivity:

Go outside and find a tree to study. Smaller and simpler trees are better for this exercise. Count how many orders of branching the tree shows. It’s very difficult to count all the higher-order branches on a tree, so we’ll focus on the first few orders.
Fill out the tables below:

Tree 1
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Now, find a different tree of the SAME species, and repeat your data collection for this tree:
Tree 2
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Finally, find a tree of a DIFFERENT species, and repeat your data collection for this tree:
Tree 3
How many zero order branches are there? [ ]
How many first order branches are there? [ ]
How many second order branches are there? [ ]
How many third order branches are there? [ ]

Do your results match the idealized drawing of Leonardo’s tree? [ ]
Do the two trees of the same species have the same number of branches of each order? [ ]
Do the trees of different species have the same number of branches of each order? [ ]

Fractals in the Body

Not only are fractals in the world all around us – they are even INSIDE us! In fact, many of our internal organs and structures display fractal properties.

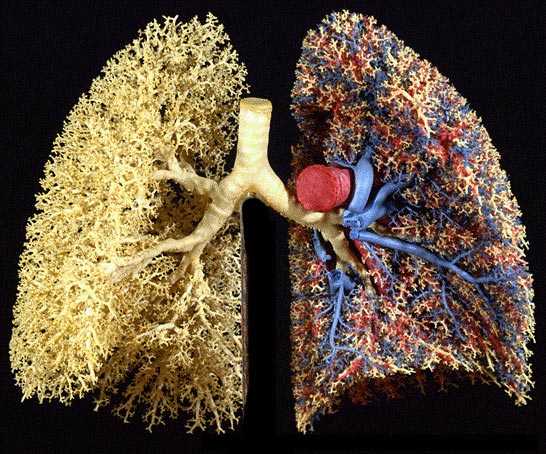
Cast of human lungs, showing blood vessels on one side. Photo courtesy Ewald Weibel, Institute of Anantomy, University of Berne.

The lungs are an excellent example of a natural fractal organ. If you look at the tree upside-down (mouse over the image), you can see that the lungs share the same branching pattern as the trees. And it is for good reason! Both the trees and lungs have evolved to serve a similar function – respiration. Since they perform a similar function, it should not be surprising that they share a similar structure. This common concept in science is known as the Structure-Function Relationship. Many of the fractals in biological systems we will explore have evolved their structures in order to perform extraordinary functions. In the case of Lungs and Trees, they both breathe. In animals, the lungs breathe in oxygen and breathe out CO₂. In plants, the process happens in reverse. Thus animals and plants are two halves of the same respiratory cycle. But here’s the key to their shared structure: They both need a large surface area to function well. The amount of gas (O₂ and CO₂) that can be exchanged through the leaves on a tree or the lungs in an animal is directly proportional to their total surface area. Although the volume of a pair of human lungs is only ~4 – 6 litres, the surface area of the same pair of lungs is between 50 and 100 square meters. That’s about the same area as a tennis court!

Note: Remember that natural fractals do not conitnue their branching forever. In human lungs, there are 11 orders of branching, from the trachea to the alveoli at the tips of the branches.

Surface Area : Volume Ratio

In non-fractal shapes, from traditional geometry, there’s a simple and important relationship between surface area and volume. Let’s examine the surface area to volume ratio for a sphere, a simple, non-fractal shape. The surface area for a sphere, SA = 4πR², and the volume of a sphere, V = 4/3πR³. So the ratio of SA / V is simply 3/R, as the π‘s and most of the the R’s cancel out. This is an inverse function, and it means that when R is large, the SA:V ratio is small, and when R is small, the SA:V ratio is large. We can plot the relationship, and see that it forms a hyperbola.

Questions:

What is the SA:V ratio for our lungs? [     ]

Assume the lungs have a Surface Area of 100 m² and a Volume of 5 liters. Give your answer first in m²/L

Now, to make this measurement more useful, we need to convert liters to cubic meters. There are 1000 liters in a cubic meter.
Calculate the Surface Area : Volume ratio of the lungs in m²/m³ [     ]

Remember the formula for SA : V for a sphere is 3/R.
How small must a sphere be to have the same SA : V ratio as our lungs? R = [     ]

The lesson? Fractal branching geometry provides an incredibly useful way to make a very large surface area extremely compact. To breathe, our lungs need a surface area the size of a tennis court. Imagine if we had to carry around with us big, flat, non-fractal lungs 10 meters wide and 10 meters tall! Thank goodness for fractals!

Fractal Blood Vessels

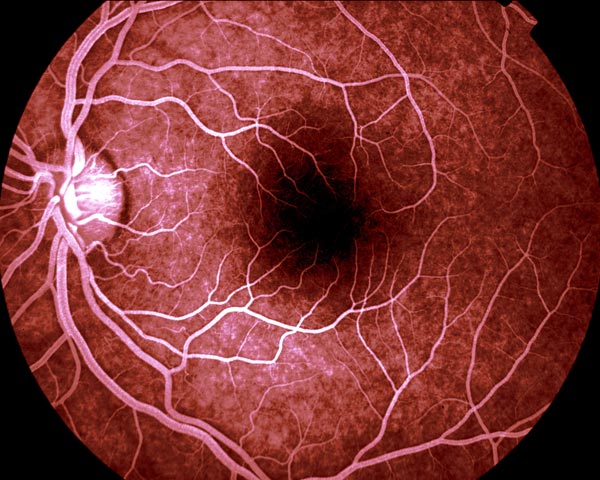
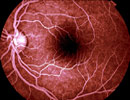
Human retina. Image courtesy of Paul van der Meer.

There are many more examples of fractal branching patterns in our bodies, and blood vessels are one of the most impressive examples. Every cell in the body must be close to a blood vessel (within about 100 microns) in order to receive oxygen and nutrients. The only way this is possible is through a fractal branching network where blood vessels branch and branch ever smaller, down to the width of a capillary, which is about 8 microns in diameter.

Depending on how they’re measured, humans have about 150,000 kilometers of blood vessels – enough to go around the world several times! (Remember, most of these are microscopically tiny capillaries.)

Are you skeptical about this enormous length? Well, let’s try to verify it.
According to one study, there are about 250 capillaries/mm³ of body tissue.^REF And according to another study, the average length of a capillary is about ~600 microns, just over half a millimeter.^REF

Using these numbers, we can compute an estimate of the total length of capillaries in a human.

Questions:

• How many capillaries are there in a cubic millimeter? [ ]
  
• How long is each capillary, in millimeters? [ ]
  
• What is the total length, in millimeters, of capillaries in a cubic millimeter of body tissue? [ ]
  
• Next we need to figure out how many cubic millimeters there are in the human body.
• How many cubic millimeters are there in a cubic centimeter? [ ]
  
• How many cubic centimeters are there in a liter? [ ]
  
• One liter (of water) weighs 1kg, and assuming the body weighs 100 kg, how many liters are then in the body? [ ]
  
• So how many cubic millimeters are in the body? [ ]
  
• Then how many millimeters of capillaries are then in a 100 kg body? [ ]
  
• How long (in millimeters) are the capillaries in one liter of human tissue? [ ]
  
• How long is this distance in meters? [ ]
• How long is his distance in kilometers? [ ]

The answer you should get is not quite as long as the number cited above, but that is probably because we’re only counting the smallest of the blood vessels, the capillaries.

Note: From this exercise, you can see why scientists generally like to use metric units – imagine how much more cumbersome this calculation would be if we used inches and pounds for our units!)

Insects have a very different respiratory and circulatory system than mammals. Because of their much smaller size, they have a much larger surface area to volume ratio than bigger animals. This allows them to take in oxygen passively through small holes in their bodies called spiracles which branch out into their body tissues, and eliminates the need for lungs to drive the respiration process. Their passive respiratory system helps put an upper limit on the size of insects^REF, and explains why (except in horror movies^REF) we don’t see giant insects the size of cats or dogs!

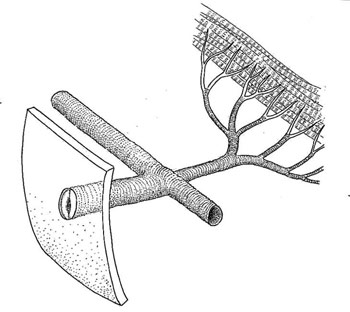
The respiratory system of an insect consists of a network of branches emanating from holes called spiracles.
Photo courtesy of Don Mackean, Biology Resources.com.

Fractal Rivers

“All the branches of a watercourse at every stage of its course, if they are of equal rapidity, are equal to the body of the main stream. – Leonardo da Vinci

Once again, Leonardo anticipated the discovery of fractal geometry by his insightful analysis of natural systems.

Much like the circulatory system in the body, the planet Earth has fractal river networks that transport rainfall from the land to the oceans. Like all fractals, these complex, self-similar patterns are formed by the repetition of a simple process over and over. In the case of a river network, it is formed by rain falling and then flowing down hill. Erosion occurs, which forms a small channel, and then the next time rain falls it will follow the same path, and carve the channel a little bit deeper. Erosion is very powerful, but very slow.

One of the remarkable properties of a river network is that it collects a huge amount of rainfall from a very large land area and condenses it into a small area. This explains how a river can keep flowing, even when it hasn’t rained recently in the vicinity. It may have rained somewhere hundreds of kilometers upstream along one of the tributaries. We will learn more about the important concepts of watersheds and drainage basins in Chapter 8, on Fractal Geography.

Self-similar river network from the Shaanxi province in China. Scale is 300 km across. Colors represent elevation.
Image Courtesy Bruce D. Malamud, Kings College London.

The processes that create rivers are not confined to Earth. The photo below shows a similar drainage network on the planet Mars, strongly suggesting the presence of rainfall in the distant past.

Presumed ancient river networks on Mars. The scale is 160 kilometers across. Viking Orbiter image 606A56, centered at 42.5°S 92.6°W.
Image processing by Brian Fessler (Lunar and Planetary Institute). Image courtesy NASA.

Fractal Lightning

Another naturally occurring fractal pattern is a lightning bolt. As Benoit Mandelbrot noted in the opening quotation, lightning does not travel in straight lines. Rather, it follows a chaotic, jagged path, formed as the huge charge separation built up in the sky suddenly breaks down.

The majority of a lightning bolt is generally hidden in a cloud, much as an iceberg hides beneath the ocean. Lightning can be very large, spanning several kilometers, but it is formed in microseconds. Thunder is a fractal sound. It is caused by the superheating of air. Because the pathway of the lightning bolt is a jagged fractal in 3D space, the time it takes to reach your ear varies, and the thunder rumbles in a corresponding fractal pattern.

Lightning over Albuquerque, New Mexico. Photo courtesy of Jef Duncan.

Lightning can also be created in a laboratory, at small scale. By using a particle accelerator to charge up a piece of acrylic material electrons, and then suddenly discharging it, a lightning-like discharge path is created and burns a trace in the material. It appears like frozen lightning.

A Lichtenberg Figure, or simulated lightning, created by rapidly discharging electrons on a block of acrylic. Scale = 10 cm.
Photo courtesy of Bert Hickman, Teslamania.com.

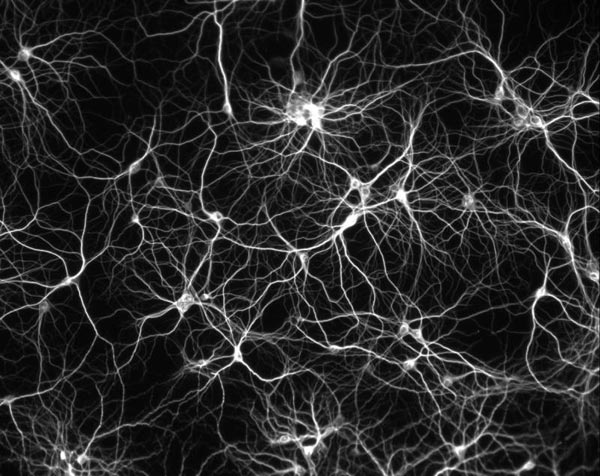
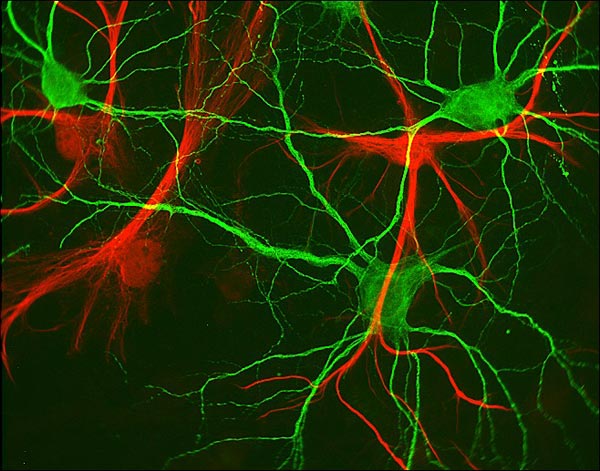
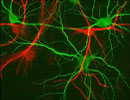
Fractal Neurons Our brains are full of fractals! In fact, they couldn’t function if not for fractal geometry. The human brain comprises approximately 100 billion neurons. Amazingly, there are about 100 trillion synapses, or connections, among these brain cells. That’s an average of 1000 connections for a given cell, though some neurons may only make a single connection, while others may have hundreds of thousands of synapses with cells all over the brain. The axons reach out to make synaptic connections with the dendrites of other neurons. It is the fractal branching pattern of the neuron’s axons and dendrites that allows them to communicate with so many other cells. If neurons were shaped like cubes and neatly packed into the brain, one neuron could only connect with at most 6 other cells. Hippocampal neurons. Scale approximately 700 microns. Image courtesy of Paul de Koninck, Universite Laval. Hippocampal neurons (green) and glial cells (red). Scale approximately 90 microns. Image courtesy of Paul de Koninck, Universite Laval.   Human brain showing the convoluted cortex. Image courtesy of Wikimedia Commons. Question: According to these values, how many kilometers of axons are there in the entire cortex? [     ] In Chapter 5, Chaos, we will explore with a simulator the firing patterns of individual neurons which themselves can behave chaotically.

Spirals The logarithmic or equiangular spiral is one of the most beautiful forms in nature, and it occurs in a wide variety of systems and at an enormous range of scales. No matter what the size, the shape of a given remains the same. Different spirals may twist at different rates however, and the twistedness is governed by the parameter τ in the following equation that defines the spiral in polar coordinates: r = eτΘ, where r is the radius and Θ is the angle. Computer animated spiraling vortex. Applet courtesy of Jared Tarbell.   Spirals in Nature Galaxies are the largest examples of spirals known. A single spiral galaxy may contain a trillion stars. Interestingly, there is a relatively uniform distribution of stars in a spiral galaxy. In other words, the spiral arms do not contain a greater number of stars. Rather, the spiral arms are brighter because they contain many short-lived extremely bright stars, formed by a rotating spiral wave of star formation. The waves of star formation are made visible because they contain many young and very bright stars that only live a short time, perhaps 10 million years, as compared to the more common stars, such as our sun which live for several billion years. M51 the “Whirlpool Galaxy”. Scale approximately 100,000 light years. Image Courtesy Nasa. Hurricanes or typhoons (also called cyclones in the southern hemisphere) are the largest spirals here on Earth. The largest of these storms on record was Typhoon Tip, which measured 2170 km in diameter. In the north, they spin counterclockwise, while in the south they spin in the clockwise direction. Hurricane Katrina, 2005. The state of Florida is visible for scale. Image courtesy NWS. The plant kingdom is also full of spirals, as evidenced in many cacti, flowers, fruit, pinecones, etc. Agave Cactus. Image courtesy of Francesco Hamamatsu. Sunflower (Helianthus annuus). Image courtesy of Wikimedia Commons. A nautilus shell serves to illustrate the simple, repetitive process that creates a spiral. The organism keeps expanding its home by adding sections to its shell. Each section is a little bigger than the one before, and a little bit rotated. The scaling factor and the rotation angle remain the same at every step in the process. It is this simple combination of rotation and expansion that creates the spiral, and accounts for its ubiquity. Nautilus shell. Image courtesy of Wikimedia Commons. We will revisit spirals in nature in Chapter 11, when we explore the Fibonacci Sequence, a common and beautiful numeric pattern in nature which creates the Golden Ratio. Question: How many segments are there in one full rotation (360 degrees) of this shell? [ ] What is the angle, in degrees, occupied by one segment?  [ ] Exercise: Order the following fractals by scale, from smallest to largest:[ ] [ ] [ ] [ ] [ ] [ ] A B C D E F Remember: Fractals transcend scale. Fractals occur over a wide range of sizes in nature, from the microscopic to the galactic – AND at all time scales, from nanoseconds to millions of years.