
We saw in the previous section that nature is full of fractal patterns. Many of these structures take on branching or spiraling patterns, and we saw how simple processes, repeated over and over again, could create these complex patterns. In this chapter, we will explore these same sorts of repetitive process, but this time in the realm of pure geometry. We will learn about the power of iteration to create complex fractal patterns, through the exploration of Iterated Function Systems, and we will see some of their extraordinary properties. We will even learn the special language of L-Systems that describes how we can iterate simple systems to create realistic plant-like structures.
Sierpinski Fractals
There are many ways to generate geometric fractals. First we will begin with the process of repeated removal, and an exploration of the Sierpinski Triangle.

Starting with a simple triangle, the first step, shown in the figure, is to remove the middle triangle. This leaves behind 3 black triangles surrounding a central white triangle (iteration 1). We can then repeat the same process, at a smaller scale, and remove the middle third of each of the three triangles, giving us the second iteration. At this level, we have 9 smaller black triangles remaining. The number of smallest triangles triples again in the third iteration, to 27. Level 4 has (27 * 3) = (9 * 9) = 81 tiny triangles.
The progression continues tripling, and the number of triangles, T, can be expressed as: T=3n
One great thing about geometric fractals is that they never need to end, they can keep on repeating forever! This allows us to zoom deep into these fractals and find ever more detail.

Questions:
How many smallest black triangles will there be at the 5th iteration? [ ]
How many smallest black triangles will there be at the 8th iteration? [ ]
Another fractal we can make using the process of repeated removal is the Sierpinski Carpet. To create this shape, we start with a square, divide it in 9 smaller squares and remove the central square. Then repeat the process with each of the remaining 8 squares.

5th order Sierpinski Carpet
There is one 1’st order white square and nine 2’nd order white squares in the figure above.
How many of the smallest white squares will there be at the 5th iteration? [ ]
How many 6th order squares would there be if we continued the process? [ ]
There are two ways to solve these problems. The first way is to discover and use a formula that tells you how many squares are created at a given iteration.
The second method is simply to count all the squares at a given size.
If it took you 1 second to count each square, regardless of its size, how long (in minutes) would it take you to count all the white squares in the image above? [ ]
How long (in minutes) would it take you to count all the squares in a 6th order Sierpinski Carpet? [ ]
Sierpinski Fractals – in 3D
Now let us continue exploring these fractals in 3 Dimensions. (Although we’ll learn in Chapter 9 on Fractal Dimensions, that these objects are not quite fully 3-Dimensional!)
The Sierpinski Tetrahedron (sometimes called the Tetrix) is created by starting with a tetrahedron and removing the middle tetrahedron, and then repeating this process, just as we removed the middle triangles to form the Sierpinski Triangle.
Click and drag the Sierpinski Tetrahedron above to rotate it. Play with it to get a feel for it from different angles.
Next, <Ctrl>-click the shape to lower the number of iterations, eventually reaching a simple tetrahedron, the 0’th order. <Alt>-click the shape to raise the number of iterations. The 1’st order shape is made of 4 tetrahedrons. Play with this shape, and then <Alt>-click to generate the 2’nd order shape. (Be careful not to go too high or you will crash your browser!)
Questions:
How many of the 2’nd order tetrahedrons are there? [ ]
<Alt>-click the shape a few more times to raise the number of iterations. Create a formula to tell you how many tetrahedrons exist of a given order.
How many of the 6’th order tetrahedrons are there? [ ]
Now let’s explore the surface area and volume of the Sierpinski Tetrahedron.
The formula for the surface area of a plain tetrahedron is:
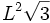
where L is the length of one edge.
How do we calculate the surface area of the first order Sierpinski Tetrahedron? Well, it’s made up of 4 copies of the original tetrahedron, where the length of each edge is only half of the original length,
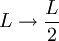
So if we substitute L/2 in the formula for the area, we can find the area of one of the smaller tetrahedrons. But, there are four of these tetrahedrons, so we have to multiply the area by 4.
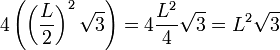 |  |
This tells us that the area of the 1’st order Sierpinski Tetrahedron is the SAME as the area of the 0’th order Tetrahedron. We can continue this process, and discover that the surface area decreases by a factor of 4 each iteration, and the number of tetrahedrons increases by a factor of 4. This means that the surface area stays the same at each iteration.
The total volume, of the Sierpinski Tetrahedron however, decreases by a factor of 2 at each step. At the logical limit of infinite iterations, the volume decreases to zero, but the surface area remains constant.
This is a very strange property!
Questions:
If the surface area of a 2’nd order Sierpinski Tetrahedron is 100 cm2, what is the surface area of the 4th order shape? [ ]
If the Volume of a 0’th order Sierpinski Tetrahedron is 256 cm3, what is the Volume of the 5th order shape? [ ]
Now let’s translate the square Sierpinski Carpet into the cubic fractal know as the Menger Sponge. Another name for this could be the Sierpinski Cube.

Again, we can click and drag the object above to rotate it. Play with it to get a feel for it from different angles.
Next, <Ctrl>-click the shape a couple of times to lower the number of iterations, reaching a simple cube, the 0’th order. <Alt>-click the shape to raise the number of iterations. (Again, don’t go too high or your computer will struggle to render the image!)
Interestingly, it can be shown that the Surface Area of the Menger Sponge increases with each iteration, while the Volume decreases with each iteration. Thus, at the logical limit of infinite iterations, the Volume goes to 0, and the Surface Area goes to infinity (∞). Again, this is a very strange property!
The 1’st order shape is made of 20 smaller cubes, and the 2’nd order shape is made up of 400 tiny cubes.
Question:
How many of the smallest scale cubes are in the 3’d order Menger Sponge? [ ]
Play with the cubic fractal above. <Ctrl>-click the shape a couple of times to get to the 0’th order cube. Figure out the process of removal that generates this fractal.
Questions:
- How many cubes are in the 1’st order shape? [ ]
- How many cubes are in the 2’nd order shape? [ ]
- How many cubes are in the 3’nd order shape? [ ]
Iterated Function Systems
In this section we will learn a different way to create geometric fractals. Instead of repeated removal as in the Sierpinski fractals, we will now explore the process of Repeated Substitution. These types of fractals are called Iterated Function Systems, or IFS Fractals.

The sequence above shows the development of the Dragon Curve fractal, which is formed by repeated substitution. The image on the left, labeled ‘0’ is called the generator. The first iteration is formed by replacing each half of the dragon curve with a smaller copy of the same shape, rotated to fit. This process keeps repeating, where each iteration has twice as many copies of the original generator.
Click the box above to step through the iterations of the Dragon Curve. (Reload the page to start over.)
Question:
How many line segments are in the 4th order shape? [ ]
Next we’ll explore a famous IFS fractal known as the Koch Curve. Here the generator is simply a line with a triangular bump in it, shown below.
Change the iteration number in the control panel at the top right of the applet. At iteration 2, each of the 4 line segments in the generator is replaced by a copy of the generator. In Chapter 9, when we explore fractal dimensions, we will revisit this curve and learn how the length increases with each iteration, until it eventually becomes infinitely long!
We can create Iterated Function System fractals with more complicated generators, as in the two examples above. Click on each of them to see them evolve. In the next lessons, we will learn about Lindenmayer Systems, which provide us with a language to define the substitutions at each iteration. Also known as L-Systems, they allow us to use the process of iteration to replicate the forms of many common plants.
Lindenmayer Systems (L-Systems)
In this lesson, we will use a java applet, called “Fractal Grower” in a separate window to explore the language of L-Systems. This simple but powerful language allows us to harness the power of iteration to create realistic looking plant-like structures, as well as many other interesting fractals.
Before we launch the Fractal Grower program, we’ll look at the basic grammar of the L-System language.
Let’s examine the growth of an extremely simplified tree.
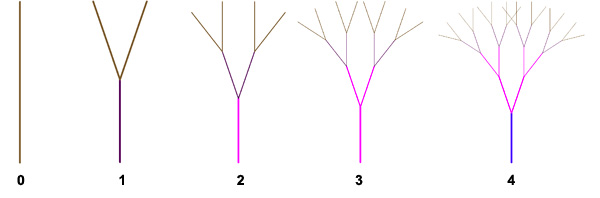
In the 0’th iteration, we have a straight vertical line. We call this starting condition the ‘axiom,’ and we will denote this line with the symbol ‘f’.
Next we will apply a rule to the line f, and in this case, the rule is to split apart and form two new branches. We will describe this rule as:
This rule means that the next iteration will consist of a line ‘f’ with a branch ‘f’ angling to the right (+) and a branch ‘f’ angling left (-).
We then apply this rule again, recursively, to each of the new branches, creating the next iteration (2) in the figure above. We keep repeating this process again, with each of the new branches, to create the 3’d and then the 4th iterations of the tree.
Notice how iteration 3 consists of two copies of iteration 2, and iteration 4 consists of four copies of iteration 2. Thus we can see that the L-System rule creates self-similar patterns.
After opening the program, choose the option to “Start in Full L-System mode”. The applet then launches in a big display window and a smaller control panel.
From the top of the control panel, you can access a number of preset L-Systems. Choose the one called “Twig”. Use the “Previous” and “Next” buttons at the bottom to raise or lower the number of iterations. Adjust the slider labelled “Turn Angle”. Adjust the other sliders to see what they do.
Note the panels that display the Axiom and the Rules. These fields are editable, and you may feel free to experiment with changing the axiom and the rule.
There are a few more symbols to know about. the letters a-f determine what color the line will be drawn.
The ‘!’ symbol tells the program to scale the lines at each iteration, which is controlled by the ‘Growth’ slider.
The symbol ‘g’ is an invisible line, useful for creating blank spaces in a pattern.
On the next page, we will do some exercises to create fractal patterns of your own.
Lindenmayer Systems (L-Systems)
If it’s not open already, Click to launch Fractal Grower
We’ll start by exploring some of the preset L-Systems to try to approximate some natural fractal plants.


You can use the “Twig” preset with a Turn Angle of 60 degrees to create the image on the top right
Play around with the sliders in the various presets to create a few other shapes that resemble familiar plants.
In the following exercises you will be creating fractals in the Fractal Grower program, and will be saving images you create, and pasting them into a solution document that you will email to your instructor. (?)
To capture an image, first shrink the main Fractal Grower window to about 3 inches wide. In Windows XP, use <Alt>-printscreen to capture the Fractal Grower window. In Windows Vista, use the Snipping Tool, and in Mac OS X use Apple-Shift-4. (Make sure to shrink the window before capturing, as otherwise the images will be too large for emailing.)
1: Turn Angle, Growth, and the Symbols f and !
Figure A below shows generation 7 of the Twig preset. (The image is shown on a white background so that if this document is printed, it will use less ink than it would if the background were black.) There are two types of lines in the Twig preset: Lines drawn by the “f” symbol (These are the tips of the branches) and lines drawn by the “!” symbol. The growth slider has no effect on the length of “f” lines, but changes the length of lines drawn by the “!” symbol. In particular, when growth = 1, “f” lines and all “!” lines have the same length. When growth is larger than 1, “!” lines get longer with age. New “!” lines are always the same length as “f” lines, but older “!” lines get longer and longer. What do you think is meant by older “!” lines? This idea of symbol age is describe in the on-line help, but see if you can figure out what means by playing with the software.
 |  |
| Figure A: Generation 7 of Twig preset | Figure B: Generation 7 of variation of Twig preset |
Assignment:
- By changing the turn angle and growth value it is possible to morph figure A into figure B. Do so, and record the required values of Turn Angle and Growth.
- Starting with the Twig preset, make modifications to the Turn Angle, Growth and Start Angle until you create an image you think is cool. Capture the image and paste it into your solution document. Record the parameters you used to create the image.
- Starting with the Twig preset, make modifications to the Turn Angle, Growth and Start Angle until you create an image you think is cool. Capture the image and paste it into your solution document. Record the parameters you used to create the image.
2: Drawing with Fractal Grower
Next, let’s become familiar with how to define the starting shape or axiom in Fractal Grower. We can use the procedure of drawing line segments ‘f’ and then rotating with the ‘+’ or ‘-‘ symbols to draw any simple pattern we wish. You can think of the image as being drawn by a turtle following simple instructions, forward, left, and right. Play in the axiom editor, and practice!
Let’s start with a relatively simple exercise, and draw your initials. You’ll use the first iteration for this exercise, so only the axiom matters, not the rule. You will need to carefully choose your Start Angle and Turn Angle.

The author’s initials, created with the axiom:
af-f–f-ff–f++++ff++gbff—ff+++ff—ff
Assignment:
Capture the image of your initials, made in Fractal Grower. Paste it into your solution document. Include the axiom you created.
3: Changing the Rules
Figures C and D show generations 1 and 4 of the Fern preset. The axiom for this preset is “f“, a single line. The preset has one rule that replaces the “f” with four stem segments (the four “!” symbols in the rule) and with seven branches (three on each side and one at the tip).
Change the Fern preset rule so that only 4 branches are created. Also change the angle of the branches so that some of the branches are narrower and others are wider. Figure 6 shows an example of generation 7 of the fern preset with only 4 branches and with the relative branch angles changed. You may choose to remove a different three branches. Note: adjustments to the Turn Angle slider change all of the angles and make all larger or all smaller. To make some angles smaller and some larger, you need to change the production rule. Create a fern with 4 branches and a set of branch angles that you find pleasing. Paste a cropped screen capture of generation 1 and a cropped screen capture of a higher generation into your solution document. Record in your solution document the parameters (axiom, rules, turn angle, start angle, and growth) of your creation.
 |  |  |
| Figure C: Generation 1 of Fern preset | Figure D: Generation 6 of Fern preset | Figure E: Generation 7 of Fern preset with 3 branches removed and relative branch angles changed. |
Assignment:
Create a fern with 4 branches and a set of branch angles that you find pleasing. Paste a cropped screen capture of generation 1 and a cropped screen capture of a higher generation into your solution document. Record in your solution document the parameters (axiom, rules, turn angle, start angle, and growth) of your creation.
